chaosophia218:Unveiling the Mandelbrot Set.Back in the 1970s and 1980s, mathematicians working in an
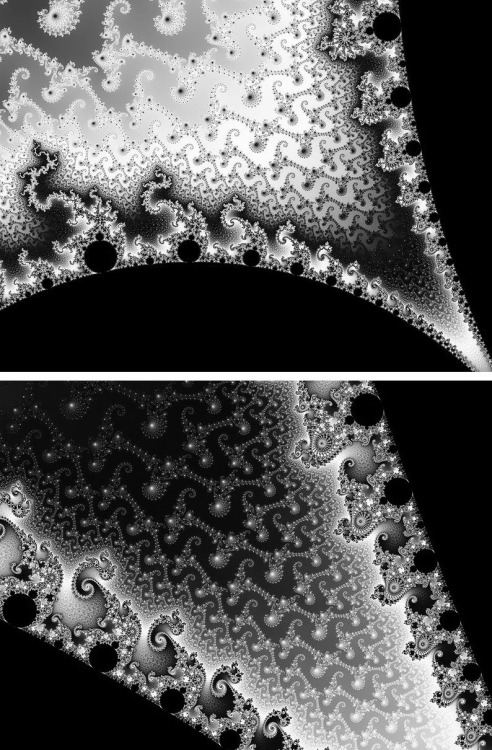
chaosophia218:Unveiling the Mandelbrot Set.Back in the 1970s and 1980s, mathematicians working in an area called dynamical systems made use of the ever-advancing computing power to draw computer images of the objects they were working on. What they saw blew their minds: fractal-like structures whose beauty and complexity is only rivalled by Nature itself. At the heart of them lay the Mandelbrot set, which today has achieved fame even outside the field of dynamics. The Mandelbrot set is a fractal. Fractals are objects that display self-similarity at various scales. Magnifying a fractal reveals small-scale details similar to the large-scale characteristics. Although the Mandelbrot set is self-similar at magnified scales, the small scale details are not identical to the whole. In fact, the Mandelbrot set is infinitely complex. Yet the process of generating it is based on an extremely simple equation involving complex numbers. The Mandelbrot set is an incredible object that equals infinity. It’s really amazing that the simple iterated equation Z = Z^2 + C can produce such beautiful works of mathematical art. -- source link