isomorphismes: In trying to understand sheaves, topology, open sets, chain complexes, kernel( ∂
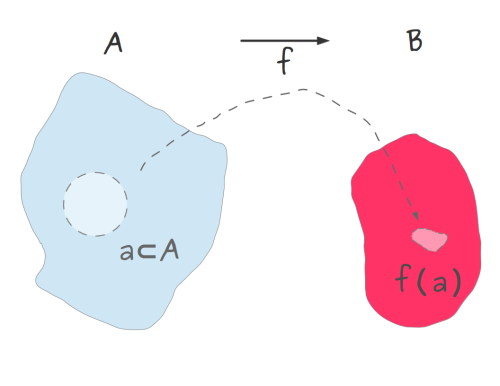
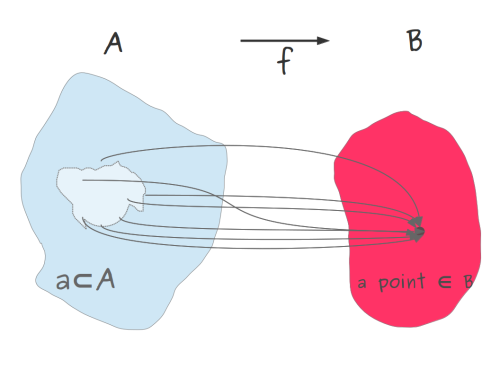
isomorphismes: In trying to understand sheaves, topology, open sets, chain complexes, kernel( ∂) ÷ image( previous(∂)), algebraic topology, cokernel, fibration, base space & total space, étale maps,, and some other stuff, I found I needed to think more simple, dumb thoughts, carefully aboutpartial functionscodomain vs imagethe Cartesian definition of a functionmonotonicity / injective / horizontal line test / multimapsSometimes the image of ƒ might take up less than the entire range defined. Sine from ℝ to ℝ is an example; the height of the wave never goes above 1 or below −1 (since the function is defined, for convenience, on radius 1 “unit”. Whether that be millimetres or kilometres is left unstated, to make theory easier).Square root from ℝ to ℝ is an example of both: neither can we assign values to negative inputs (so √ is only a “partial function”) — nor will we get negative outputs (unless we violate the Cartesian definition of function, or at least tweak it).(it’s in this sense that ℂ is a “better” number system: any root √ ∛ ∜ , if defined to accept & return ∋ ℂ , will work on any input, and, we will actually use all of the output values we allotted ourselves (so image won’t be smaller than range≝codomain. Since ℂ is kind of circular, roots just end up changing how many angles θ you go around the unit exp(√−1 • θ). Look up the power/log/exponent rules and you’ll see what I mean. ℂ numbers also have a length but √ does the same thing to that, that it did to the ±-only ℝ numbers. And it’s a (positive-only) length, so no patial-function crap or range/image mismatch there. ).ker ( ƒ ) ≝ ƒ⁻¹(1)Let ƒ be a function from X to Y. The preimage or inverse image of a set B ⊆ Y under ƒ is the subset of X defined by The inverse image of a singleton, denoted by ƒ−1[{y}] or by ƒ−1[y], is also called the fiber over y or the level set of y. The set of all the fibers over the elements of Y is a family of sets indexed by Y. -- source link