realworldmath:What the hell is knot theory? Knot theory is one of those fields in mathematics that
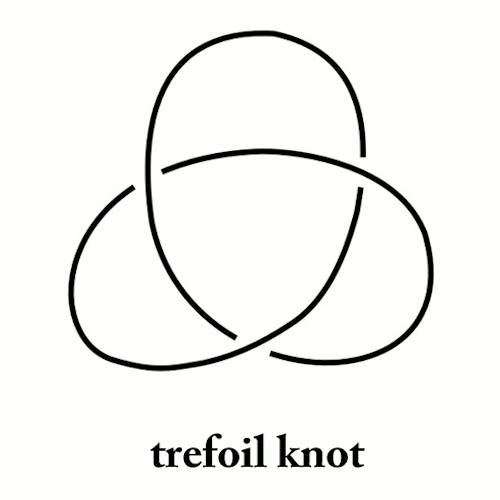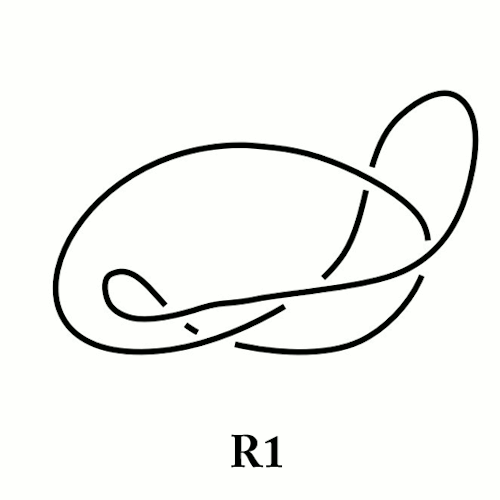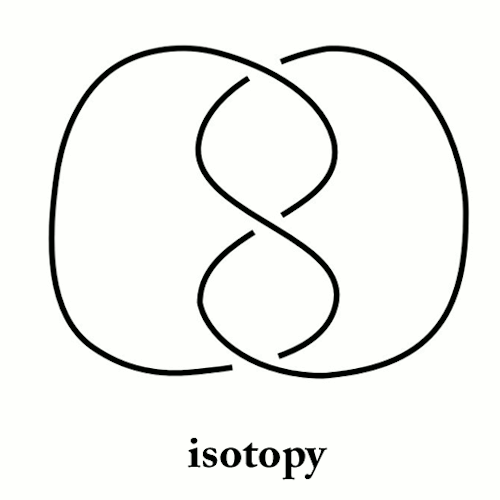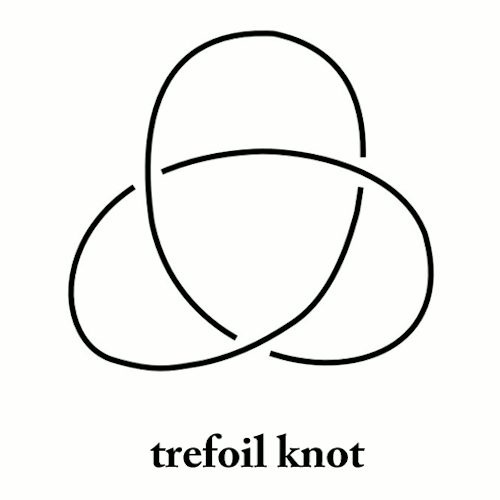
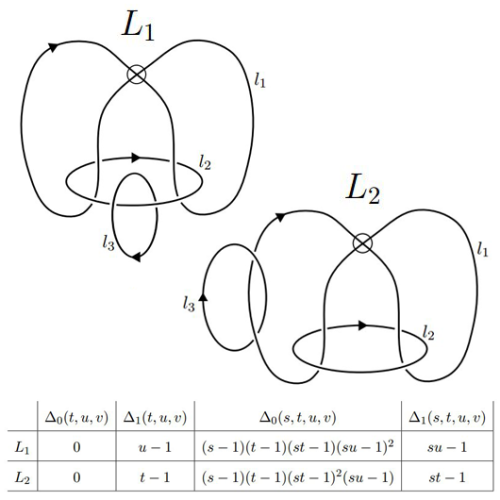
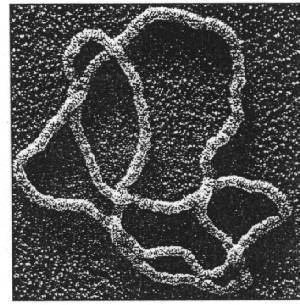
realworldmath: What the hell is knot theory? Knot theory is one of those fields in mathematics that falls squarely into the camp of “totally random seemingly useless but actually really cool”. Borne out of the flawed theory that atoms are knotted vortices in the aether of space, what is now known formally as knot theory was first considered by the British Physicist Lord Kelvin in the late 1800s. By the time Kelvin’s physical model had been proven incorrect, interest in knot theory had already gained traction among some of Europe’s most innovative mathematicians. Since then, it’s developed into a full-fledged sub-field of mathematics, relating to other fields as diverse as topology, graph theory, physics, abstract algebra, and theoretical computer science. There are 3 things that make a mathematician’s knot different than a regular knot: (1) A knot’s string is one continuous loop, with each end connected to other (think of fusing the ends of your shoelaces together). (2) A knot is infinitely stretchy, flexible, and malleable. And (3) you can NEVER cut a knot, even if you glue it back together. The main problem of knot theory can be stated in very simple terms: When are two knots “different”? Or more specifically, given any two knots, is it possible to twist, contort, stretch or deform one of them (without cutting!) so that it looks like the other? If you’re like the dozens of people who I’ve explained knot theory to in the past, I know what you’re thinking: “Okay, that sounds kind of interesting. So what is it good for?” Though knot theory started out as nothing more than the curious pursuit of a few mathematicians with too much time on their hands, you’ll be surprised to know it has found real world applications in non-mathematical fields. Among other applications, it has been used to study the formation of DNA molecules in biology and may play a part in the development of quantum computers. Knot theory as a prime example of why it remains so important to study, develop, and explore new mathematics. What often starts out as an trivial game of the mind, turns out to have far reaching and unexpected applications. Full Disclosure: I wrote a thesis on a topic in Virtual Knot Theory. -- source link
#knot theory